Electric Yggdrasil

The metaphors for the shape of the world that shape the way we see the world

Gabriel Nagypal

A while ago, a good friend of mine related to me a strange conversation he’d had at the bar. His companion had insisted that the Earth is not a sphere. At first my friend assumed the guy was another tiresome flatlander, which was also my first assumption. Instead, the acidhead insisted that our planet possesses some sort of hyperdimensional geometry. This assertion left my friend baffled, which was why he brought it up to me. What could this guy have possibly meant?

Now, I have no idea what he meant. I heard of this exchange second hand, and wasn’t there to interrogate the guy further in order to probe out his meaning.

It did, however, get me thinking.

So often in these sorts of debates, we find ourselves on one side or another of a sharply divided ontological belief-set. One side stakes out a position, we claim the other, and the interaction then becomes a shoving match between two sides that are convinced that they are in possession of the truth. This is frequently unhelpful from an alethiological perspective, because when you’re quite convinced that you know what the truth is, you immediately close yourself off to the possibility that you really don’t.

Sometimes the truth is somewhere in the middle, being a compromise between the contested positions, or a synthesis of them. That isn’t so interesting, though.

In other cases, both things are true. Consider the statements ‘there is nothing new under the Sun’ and ‘all there is, is change’. Both of them point to important aspects of reality. The first relates to basic dynamics, the laws¹ of nature being invariant over time. The second indicates that everything is flow and process – in our material universe, nothing lasts forever, nothing is ever fixed, everything is always becoming something else, and indeed there are no things as such. As the weeping philosopher said, ‘No man ever steps in the same river twice, for it’s not the same river, and he’s not the same man’ ... and yet, during his life as now, there are rivers, and there are men who step in them. Plus ça change, plus c’est la même chose.

The most interesting cases are the ones in which both positions are actually wrong, or at any rate incomplete, and the tenacity of the fight between them prevents either from seeing something else that might be even more interesting.

So, take the debate over the geometry of the Earth. And yes, I’m almost as annoyed as you that this is even a debate, but bear with me.

On one side are the Flat Earthers, who insist that all of the evidence for a spheroidal Earth is simply a Freemasonic conspiracy theory. It is immediately apparent to our eyes, they say, that the Earth is flat, with a dome of heaven arcing over it. This is, they go on, further attested to in the Bible, for otherwise how could Satan have taken Christ up to the mountaintop and shown him all the lands of men? That would obviously be impossible on a ball Earth. The Bible is the inerrant word of G-d, while ‘science’ is just the flawed work of man, so who you gonna believe? QED.

Ona Kistensen

On the other side are, well, pretty much anyone who has even a rudimentary education in the natural sciences, as well as the rest of the population who still, despite everything – and this is actually quite remarkable when you think about it – still basically trust scientists. This side will point to the pictures taken of the Earth from orbit, from the Moon, and from distant spacecraft; they will point to the way distant objects disappear below the horizon²; they’ll point to the flight routes used by aircraft; they’ll point to the fact that the seasons, and the varying length of the day as the seasons change, and the amount the day length varies by depending on latitude, and the parallax of the stars, and the retrograde motions of the planets, are all perfectly explained by a spherical Earth orbiting the Sun whose axis of rotation is tilted with respect to the axis of its orbit; and they’ll mention the Greek philosopher Eratosthenes, who used a couple of sticks, the lengths of the shadows they cast, and basic geometry not just to infer the overall shape of the Earth, but to make a damn good measurement of its radius, over two thousand years ago.

The Flat Earth community has answers to every single one of those empirical observations, of greater and lesser degrees of contrivance and plausibility. To the pictures of the Earth they say ‘space is fake’. The flight paths of aircraft are part of the same elaborate conspiracy that hoaxes space exploration by hanging the ISS from balloons. To Eratosthenes’ measurements, they point out that in principle the same effect can be achieved if the Sun is much smaller and closer (which is true). To the changing length of day through the seasons, they say well, God just put the Sun on that weird looping path for His own reasons, and they give the same answer to the retrograde motion of the planets. Why the Sun should take such a path, and why such effort and expense should be taken to deceive us as to the true shape of the Earth, I’ve not yet heard the answer, although I’m sure there are speculations as numerous as Flat Earthers.

The interesting thing with Flat Earthers is that they’re actually strangely scientific in their practice, continuously coming up with various experiments with which they hope to distinguish, with their own eyes and to their own satisfaction, between the hypotheses that the Earth is flat or spherical. One of them even went so far as to launch himself in a home-built rocket (which killed him). The sad thing is that their experiments frequently return results consistent with the Earth’s surface possessing large-scale curvature. Whenever this happens they immediately start trying to identify flaws in the experiment, in order to convince themselves that the result wasn’t what it clearly was, but merely some sort of illusion produced, for example, by the uncorrected spherical aberration of a camera lens. The reason they do this is that their identities have become wrapped up with the Flat Earth community. They are the brave, intrepid, strong-minded resistance, alone possessed of the truth, alone possessing the courage to speak it in the face of the mockery and vilification of a deluded and corrupted world. Should their experiments prove that they’ve been wrong all along, their social network, indeed their very identities would evaporate like hoarfrost in the first light of dawn.

There’s a very obvious cautionary example there, for both regime-aligned mainstream narrative enjoyers and conspiracy-theorizing dissidents intoxicated on woo alike.

The presence of Flat Earthers being their goofy and occasionally obnoxious selves merely leads everyone else to roll their eyes and say, well of course the world is a sphere.

Everyone knows the Earth is basically just a spherical ball of rock.

Right?

Gourd

Well. Let’s think about that.

What is the surface area of the Earth?

The surface area of a sphere³ is 4πR^², where R is the radius. In the case of the Earth, the mean radius is 6371 km, so the surface area should be about 510 million km^2, which indeed is the answer Google will give you.

This is much, much less than the correct answer.

What is the correct answer? I have no idea, and neither does anyone else. It is unknowable.

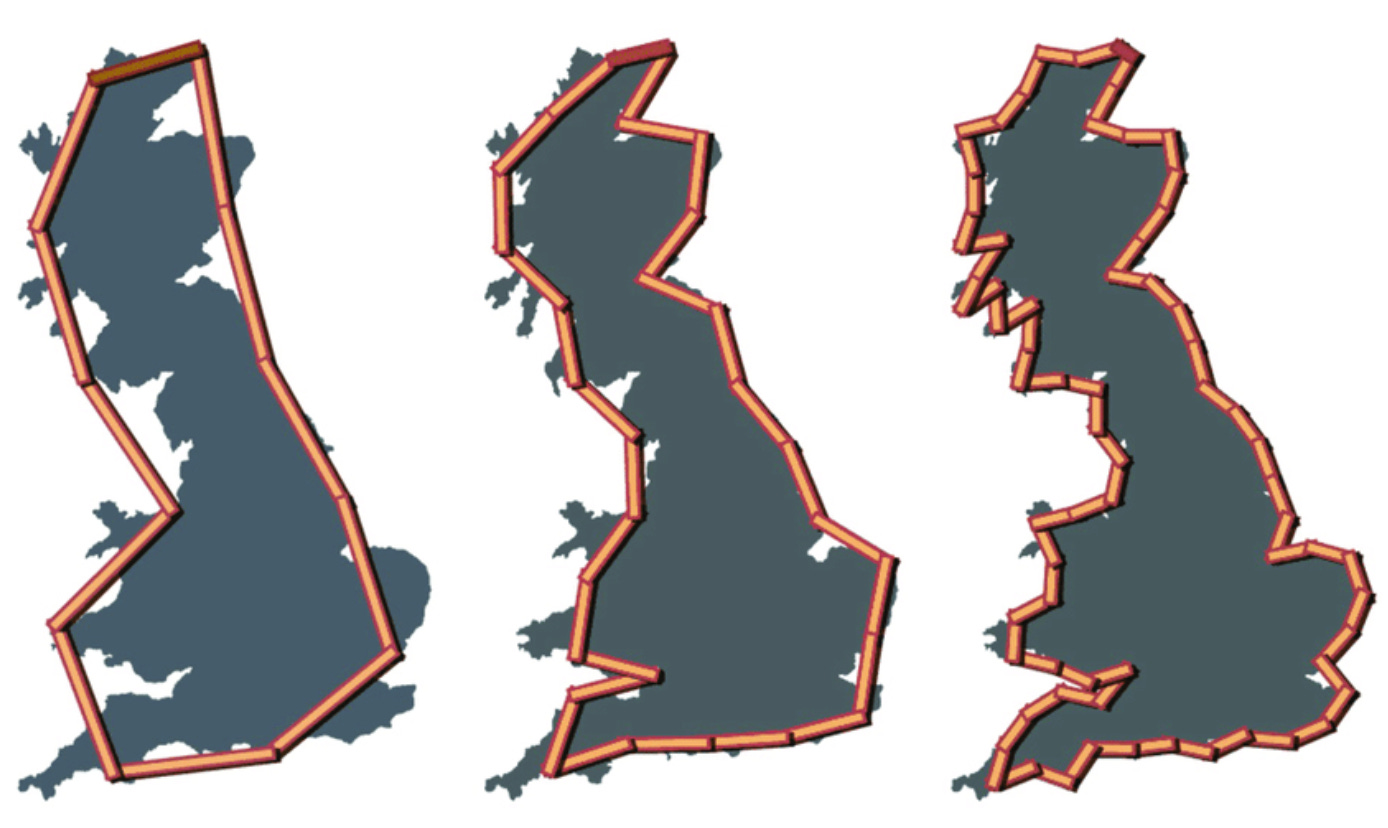
To see what I mean, consider the island of Great Britain. What is the length of its coastline? This question was asked by the great mathematician Benoit Mandelbrot in a seminal 1967 paper. In this case there’s no simple analytical formula, as there is for a simple geometrical shape like a sphere. Still, you might think that the length of the British coast is easily determined in principle. Just send a team of surveyors around, have them measure the perimeters of the various bays, inlets, beaches, cliffs, and so on, and you’ll have your answer.

Mandelbrot showed that that this doesn’t work, because the answer you get depends on the length of your measuring stick. The finer the measure, the greater the length of the coastline that you’ll find. This is because a shorter ruler will enable more detailed features to be resolved, and since the British coastline is made of atoms, that level of detail extends all the way to the atomic level.

The Koch curve

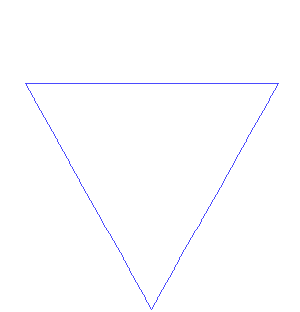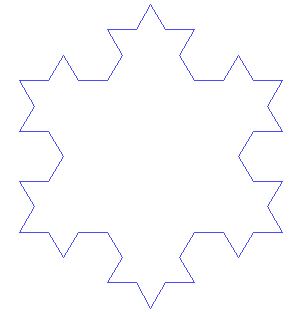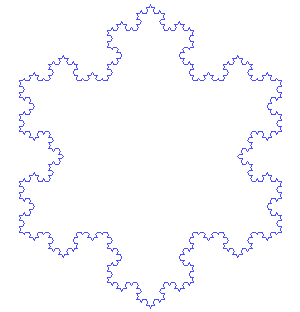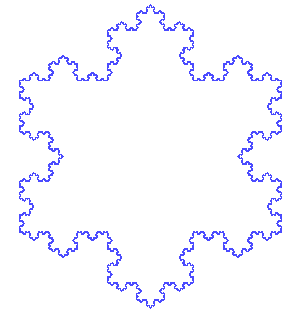
This, it turns out, is a general property of fractals – self-similar shapes that repeat the same pattern at every scale. A very simple example of a fractal is the Koch curve, which is constructed by taking a line, cutting out the middle third, replacing it with two lines of equal length to the two remaining segments of the original line, both at 60 degrees angles such that they form two sides of an equilateral triangle, and then repeating the operation an infinite number of times on each of the line segments. If the length of the initial line is unity, the length of the curve after the first step is 4/3, after the second step (4/3)^2, after the third step (4/3)^3, and so on. As is immediately obvious, if you iterate for an infinite number of steps, the length of the curve diverges to infinity.

However, if you draw three Koch curves (starting with an equilateral triangle, and performing the iterations on each side of the triangle), it is immediately obvious that the area enclosed by the resulting Koch snowflake is quite finite, despite its perimeter being infinite⁴.

Now, the British coastline isn’t exactly a mathematical fractal. Unlike the Koch curve, it doesn’t simply repeat the same structure at every scale. However, it possesses the essential fractal property of having structure at essentially every scale. The length of the British coastline is therefore quite impossible to measure, despite the area encompassed by that coast being quite well-defined.

Except, the last part of that statement only works if we assume that the surface of Great Britain is geometrically flat. Which it isn’t. I’m not talking about the Earth’s large-scale curvature, but rather about the topography. Great Britain is composed of hills and mountains, valleys and dells, meadows and pastures. Just like its coastal perimeter, its surface is highly structured, and that structure goes down to the finest level of resolution that it’s possible to discern. If you tried to actually quantify the surface area of the island, say by placing down tiles of a standard size, the answer would increase as the size of the tiles decreased. With tiles measuring a kilometre on a side, only the grossest features would be accounted for, but with tiles of a square millimetre, every small crack and stray pebble would contribute to the final result.

And of course, the same principle applies to the Earth. Its endlessly varied topography means that its surface area is, for all intents and purposes, effectively infinite.

This is quite a remarkable property of our world when you think about it. The vertical distance from the summit of Mount Everest to the lightless reaches of Challenger Deep is 19.784 km, which is about 0.3% of the planet’s radius⁵. If you were large enough to hold the Earth in your hand, it would feel as smooth as a cue ball – if the Earth were that 5.7 cm diameter cue ball, the distance from Everest to Challenger would be about 0.09 mm, somewhat finer than a human hair follicle, much too small to notice.

And yet, that unnoticeably minute deviation from perfect smoothness still manages to give the Earth an incalculably large surface area when it is taken into account.

Meaning that the Earth really isn’t a ‘sphere’ after all. A sphere is simply a sort of geometric metaphor, an approximation which captures one very important aspect of the Earth’s morphology – its large-scale roundness – but leaves out something else very crucial.

This might all seem somewhat pedantic. We’re just talking about really tiny deviations from spherical symmetry, after all. But consider how thinking of the Earth’s surface in this fashion, of foregrounding this metaphor, changes your perspective on it.

To the Flat Earther, the world is a snow globe – a plate floating in space, covered in a dome. This is probably one of the oldest ways of looking the world, as it really does appear planar to our senses unless we pay very close attention and think very carefully about what we see happening. The planar world is a limited, closed, circumscribed environment, which feels to me like a sort of claustrophobic trap. Travel long enough in any given direction and you’ll bump into the edge, and that’s that. It is profoundly finite.

The spherical Earth, by contrast, is not limited in the same way – one may go anywhere on the surface of a sphere and never find the edge. But travel long enough in one direction and you’ll invariably come back to where you started. Thinking of the Earth as a sphere brings to mind a smooth, periodic geometry, a featureless form perfect just the way it is, on which life is an eternal return, where one can travel as long as one as one likes without really going anywhere at all. Our increasingly homogenized world feels more like that every day.

A fractal (or, really, quasi-fractal) Earth, on the other hand, has an infinitely varied range of nooks and crannies to poke into. One can spend a lifetime exploring it, even relatively ‘small’ parts of it, and continue to uncover wonders one has never seen before. No two parts of it are exactly identical. No matter where you go, you’ll find something new.

Giovanni Calore

You might have noticed that I tacitly assumed that by the ‘surface’ of the Earth, we mean its solid surface – dry land, and the sea bed. We could of course include the oceans, which wouldn’t really change the argument: if any surface can be described as a fractal, the gravity waves⁶ at the interface between the water and the atmosphere fits the bill. As to the atmosphere, while not obviously structured to nearly the same degree, there’s the sticky issue in that case of just where we draw the boundary between the atmosphere and ‘empty’ space. We’ll come back to that later.

Even assuming we limit ourselves to the solid surface of the Earth, do we only count the lithosphere? What about the biosphere? With the exception of tumbleweed and dandelion seeds, vegetable life is generally quite firmly attached the ground, and it is all made directly from the same stuff as the ground. By any reasonable standard, the biosphere counts as a part of the Earth, indeed quite an integral part if we consider the role it plays in the biogeochemical history of the planet.

If the topography of the Earth can be described as a fractal, the same is true for a tree, whose trunk, limbs, branches, and twigs invariably show a self-similar structure down to fine levels of detail. Trees are the quintessential organic fractal: making synthetic images of trees was one of the first artistic applications of fractal geometry (convincing generative landscapes being the other). We might almost consider the tree to be the primal symbol of fractality.

So, consider the surface area of a tree, as compared to the surface area enclosed by the volume of soil and rock that the tree mined for the minerals and organic materials with which it built itself. The tree’s surface area is vastly larger. This high surface-to-volume ratio is useful for the tree, as it is then able to capture a large amount of sunlight for photosynthesis, and bring its various tissues in close contact with the atmosphere for respiration. The analogous structure of its roots bring them into contact with as much of the soil as possible, enabling them to scour the soil for the maximum amount of mineral and organic nutrients. That surface area is also useful for all sorts of birds, mammals, arthropods, and reptiles, for whom the fractal surface of the tree provides vastly more surface on which to live.

Trees are a particularly vivid example of fractal geometry in the living world, but the principle that the biosphere increases surface area doesn’t even really require a given organism to be organized along specifically fractal lines. Grass, for example, is pretty non-fractal – each blade is just a long stem, really. Yet compare the surface area of the prairies, about the flattest topography you can find, with and without including the grass. That might seem irrelevant to you, since you’d step on the grass the same way you’d step on the dirt; it certainly doesn’t seem irrelevant to ladybugs, for whom the grass forms a forest of stalks to crawl around on.

When the biosphere is included, the solid surface area is incomparably larger than that of the lithosphere alone. It’s going too far to suggest that dramatically increasing a planet’s surface area is the point of life, but that is certainly one of the biosphere’s notable consequences – an unfolding of buried resources, resulting in vastly more surface being made available to capture cosmic energy. The geographical topographies of Earth, Mars, and Venus are similarly varied, and all are incalculably large, but the unique presence of a biosphere on Earth means that its surface area is many orders of magnitude larger than either of its sister worlds.

The activities of the noosphere, all the mining and architectural engineering that humans do, is essentially a continuation of this process. And indeed, since our buildings, bridges, electrical transmission towers, and so on are all attached to the ground, and made from the stuff that came from the ground, there’s no reason it shouldn’t be included in the calculation of the Earth’s solid surface area as well.

Sergey Baybakov

In addition to its space-filling property, biologically organized matter does something else that more inert matter does not: it grows and decays, it changes, with comparative rapidity. Of course, non-biologically organized matter changes as well. Mountains are thrust up and erode, volcanoes explode, earthquakes shift tectonic plates, waves advance and recede along the coast and pound rocks into sand, the winds push the shifting sand of the desert and snow of the arctic into dunes and drifts. The biosphere simply exhibits this temporal quality at a much higher tempo than the lithosphere. The noosphere moves more rapidly still. Human activity can excavate a mountain and unfold its minerals into a sprawling city in a matter of years. The noosphere is an acceleration and intensification of all of the properties inherent in the biosphere, just as the biosphere, really, is simply an elaboration of the animate nature of the ‘non-living’ world. This was all worked out by Vernadsky a century ago.

This brings to attention another property that a sphere does not possess: temporality. A sphere is a geometrical shape, an unchanging abstraction in the Platonic realm of forms. The Earth by contrast is best thought of not as a noun, but as a verb. It isn’t a timeless thing that just sits there unchanging in space. It is an ongoing process, a continuous Earthing, becoming itself in every moment. Not only is its fractal surface infinitely varied, that surface is in constant flux.

Still, you say – for all this complexity in space and time, the overall shape of the Earth is at least spherical, yes?

Well.

The Earth is not only a sphere of hot rock, with a thin slick of water, a wisp of air, and a scum of living stuff between. Solid, liquid, and gas make up its densest component – the fourth state of matter, plasma, makes up its largest.

The Earth has a magnetic field, sustained by the electrical currents generated by the violently churning molten metals of its core. That magnetic field reaches out around it in all directions, and traps the ambient plasma – the charged particles, naked ions and electrons, that stream forth from the Sun in the solar wind. This is the Earth’s magnetosphere, and the volume it occupies is, to put it mildly, much larger than that of the Earth’s solid body. The magnetotail – that part of the magnetosphere downstream from the solar wind, pointing away from the Earth into the solar system – extends to a distance of 600,000 km, almost 100 times the radius of the Earth’s solid component and about twice the separation between the Earth and the Moon. In comparison to the lithosphere, the magnetosphere is vast.

Despite its name, the magnetosphere is shaped nothing at all like a sphere. Its basic shape follows from the roughly dipolar geometry of the geomagnetic field – the double-lobed form that you see when you throw iron filings around a bar magnet. This symmetry is broken, however, by the magnetosphere’s interaction with the solar wind. On the dayside – the side facing the Sun – the magnetosphere is pressed down by the pressure from the solar wind. On the nightside, the solar wind instead stretches the magnetosphere out like bubblegum. If we could see it from a distance, the magnetosphere would resemble an elongated teardrop.

The solar wind hitting the dayside of the Earth’s magnetosphere.

The magnetosphere is also one of the Earth’s most dynamically mutable aspects, capable of reconfiguring itself over huge volumes in amazingly short time-spans. This generally happens when a particularly large eruption of plasma is launched into the solar wind, which when it hits the Earth’s magnetosphere, causes it to respond in kind.

Where most ancient peoples conceptualized the Earth as a flat plain, and the more mathematically sophisticated understood it to be broadly spherical, there were some who offered up a third, and to the literal modern mind very strange answer: they took the Earth to be a tree. The world-tree was described by the Siberians; the various tribes of the Aryan diaspora such as the Indo-Aryans, the Greeks, the Germans, and the Scandinavians and also by the Meso-Americans. The best-known example is preserved in the Norse eddas, which speak of the Earth as being part of the world-tree Yggdrasil, with Midgard, the world of men, at the base of the tree, the gods of Asgard in the branches, and the underworld in the roots.

Sam Flegal

I’ve often felt that there was a remarkable similarity between the branches of a giant tree, and the field lines sprouting from the geomagnetic pole and spreading out into space.

Mike Szabados

The Norse went on to speak of a giant wyrm, Nidhogg, which gnaws at the roots of Yggdrasil and will one day cause it to fall ... this seems to me analogous to the magnetic instabilities that worry away at the geomagnetic dynamo, and will one day cause the Earth’s magnetic field to collapse and reverse⁷. Despite the name, magnetic pole flips aren’t a simple process of magnetic north and south exchanging places. They take around a millennium to complete. In between the two stable dipole configurations, the magnetic field becomes extremely complex, with multiple magnetic poles appearing all over the planet; during this phase the outer boundary of the magnetosphere comes much closer to the Earth’s solid surface ... rather like a tree’s branches falling to the ground.

Even Bifröst, the bridge between Midgard and Asgard, may have a geomagnetic analogue. Bifröst is most commonly depicted as being a giant rainbow, but some of its descriptions – as being mainly red, or as composed of three colours, and as burning with flames – are quite unlike rainbows, but very similar to the aurorae borealis, the northern lights that sweep across the sky when a solar flare injects cosmic plasma into the magnetosphere and initiates a geomagnetic storm, resulting in the air fluorescing as charged particles sleet through the upper atmosphere. The very name Bifröst comes from a verb meaning ‘to shake’ or ‘to sway’, which doesn’t sound much like a rainbow, but does sound quite a bit like the northern lights.

Chris Cold

Whether these similarities in the mythology of the world-tree and the phenomenology of the geomagnetic field have any historical basis I can’t say. Perhaps the Norse imagined that the world is a tree simply because they were surrounded by forest. On the other hand, I find it very interesting that the world-tree myths seem to be particularly prevalent in the Siberian and Aryan peoples – those who live, or originated, in the North. Perhaps there was some great event, deep in the Ice Age, when a great solar storm rendered the outlines of the polar field visible to Hyperborean eyes? Or perhaps the Ice Age Civilization had a more advanced understanding of geophysics than we might believe, which left its imprint on the cosmologies of the northern peoples?

In any case, the plasma Earth does not resemble a sphere at all, but a jellyfish pulsing with electromagnetic energy, its limbs shaking in the rain of ions that pours from the Sun, shading us from solar fury, and reaching its tendrils out into the distant depths of the void. Meanwhile the solid Earth is a quasi-fractal, with non-repeating structure at every scale, continuously re-arranging itself as its elements shift, rise, fall, grow, and decay. At one scale the Earth behaves rather like a tree; at a larger scale, it even looks like one.

But that is, after all, just a metaphor.

But so is a plane, or a sphere.

In the end, any description that we choose for anything in the world, will be a metaphor. It cannot be otherwise, because thought and language are built of metaphors, all the way down. A metaphor may apply more or less closely, but every metaphor will necessarily accentuate certain aspects of a phenomenon, while ignoring others entirely, with consequences for how we relate to that phenomenon.

The plane and the sphere are both simple geometrical metaphors, emphasizing those aspects of the world that are most featureless and constant. The metaphor of a plane prioritizes the human perspective, at the cost of rendering the motions of the Sun and the planets mysterious (to say nothing of making navigation beyond the local quite difficult). The metaphor of the rotating sphere orbiting the Sun resolves these astronomical problems and aids navigation, but occludes all those features which make the Earth an interesting place to be.

The metaphor of the tree, by contrast, draws together the endlessly detailed geometry of fractals with the open-ended evolutionary processes of life, and thereby highlights the infinitely varied and endlessly varying structure of the Earth, while simultaneously wedding events on the ground in the world of men to their roots in the subterranean kingdoms below and their branches in the cosmic realms above, weaving all together into one seamless, organically connected whole. The metaphor simultaneously emphasizes detailed structure, change over time, and connectivity.

When I look at the Earth not just with my right eye but also with my left, which is to say not only with my literal-minded left hemisphere but also with my poetically inclined right, our planet resembles an electric Yggdrasil at least as much as it does a dead ball of rock.

If you’re already a paid supporter of Postcards From Barsoom, you have my deepest and most heartfelt gratitude. Your support makes my writing possible. If you enjoyed this essay, or you’ve enjoyed previous essays, and you have the resources to do so, please consider upgrading to a paid subscription. If you take out a paid sub, you might even develop superpowers. What is certain, however, is that a paid sub gets you in to Deimos Station.

In between writing on Substack you can find me on Twitter @martianwyrdlord, and I’m also pretty active at Telegrams From Barsoom

Jorge Jacinto

1. Or are they habits?

2. This is why ships have crow’s nests: the higher one’s perspective, the further one can see past the horizon established by the Earth’s curvature.

3. We’ll ignore the equatorial bulge due to the centrifugal force from the Earth’s rotation. The deviation it introduces from perfect sphericity is small (6378 km at the equator versus 6357 km at the poles, a difference of around 0.3%), and doesn’t change the calculated surface area all that much. So long as we assume the surface is smooth, that is.

4. Also notice that the perimeter of the Koch snowflake is three times the length of any one of the three Koch curves that make it up ... despite each Koch curve also having an infinite length. Infinities are weird.

5. Interestingly, this is comparable to the difference in mean equatorial and polar radii introduced by the centrifugal force from the Earth’s rotation deforming the planet’s crust.

6. These aren’t the same as gravitational waves; gravity waves arise due to the restoring force of gravity at the interface between two distinct fluid mediums.

7. Which it is in the process of doing as we speak.